- 바이토닉 투어 (Bitonic Tour)
TSP(Traveling Salesman Problem)는 잘 알려진 NP 문제입니다. 이 문제는 '여러 도시들이 있고 한 도시에서 다른 도시로 이동하는 비용이 주어졌을 때, 모든 도시들을 단 한번만 방문하고 원래 시작점으로 돌아오는 최소 비용의 이동 순서는 무엇인가?' 라는 문제로서, 그래프 이론적으로 표현하자면 '각 변에 가중치가 주어진 완전 그래프에서 가장 작은 가중치를 가지는 헤밀턴 회로를 구하라' 는 문제입니다. 특히 이 문제는 NP-Hard 임이 증명되어있고, P=NP가 아닌 이상 다항 시간으로 해를 구하는 것이 불가능하다고 알려져 있지요. (출처 : Wikipedia) 이 문제는 Brute Force 기법으로는 O(n!), DP로는 O(2^n * n^2) 의 시간 복잡도로 최적해를 구해낼 수 있습니다.
이러한 시간 복잡도로 최적해를 구한다는 것은 시간적/메모리적으로 너무 비용이 크기 때문에, 컴퓨터 과학자들은 근사해를 구할 수 있는 방법을 연구하였습니다. 지금은 흔히 SA(Simulated Annealing)나 유전 알고리즘을 이용하여 근사해를 구합니다만, TSP 경로에 일정한 제한을 두고 최적해를 구하는 것도 근사해를 구하는 방법의 일종입니다. 이 글에서 다룰 알고리즘인 바이토닉 투어(Bitonic Tour)도 그러한 TSP 제한 알고리즘의 일부입니다.
바이토닉 투어는 2차원 좌표계 상에 주어진 점들 중 가장 왼쪽에 있는 점부터 경로를 시작하여 x 좌표값이 증가하는 순으로 점을 방문하여 가장 오른쪽에 있는 점에 도달한 다음, 같은 방법으로 x 좌표 값이 감소하는 순으로 점을 방문하여 가장 왼쪽에 있는 점에 도달하는 방법으로 만든 사이클 중 가장 가중치가 작은 사이클을 의미합니다. 이러한 방법으로 만드는 사이클은 다항 시간 내에 만들 수 있음이 알려져 있습니다.
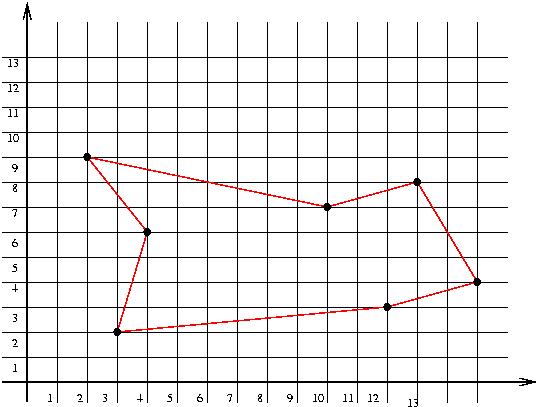

왼쪽이 TSP, 오른쪽이 바이토닉 투어로 만든 사이클입니다. 차이점을 아시겠나요? TSP의 가중치와 바이토닉 투어의 가중치가 같은 경우가 있을 수도 있겠지만, 대부분의 경우는 바이토닉 투어의 경우가 TSP보다 가중치가 클 것입니다.
이러한 바이토닉 투어의 길이를 다항 시간 내에 구하기 위해서는 어떤 알고리즘을 사용해야 할까요? 최적해를 구하기 위한 가장 중요한 아이디어는 최종적으로 구하려고 하는 바이토닉 투어가 다른 바이토닉 투어의 부분합으로 이루어져 있다는 것이지요. 이 아이디어에서 우리는 다이나믹 프로그래밍의 해법을 도출해낼 수 있습니다.
바이토닉 투어의 길이를 구하기 위한 점화식을 세우기 위해서 몇 가지 수학적인 정의 및 분석을 해 보도록 하겠습니다. 먼저 몇 가지 변수들을 정의하고 넘어가겠습니다.
여기에서 점들은 x축의 좌표를 기준으로 정렬되어 있어, p_1이 가장 왼쪽에 있는 점이며 p_n이 가장 오른쪽에 있는 점입니다.
이제 b_1i 의 값을 구해보도록 합시다. b_1i 는 p_1에서 시작하여 p_i로 향하는 바이토닉 투어를 의미하는데, 바이토닉 투어는 p_1과 p_i 사이의 모든 점을 포함하고 있어야 하기 때문에 b_1i 는 p_1부터 p_i 까지의 모든 점을 순서대로 이은 하나의 길을 의미합니다.
다음은 b_i-1,i 를 구하고자 합니다. 이 바이토닉 투어에서는 p_i-1 에서 시작하여 마지막엔 p_i로 향하게 되는데, p_i-1 은 무조건 왼쪽을 향하기 때문에 p_i는 p_i-1 과는 연결될 수 없습니다. 둘이 연결되어 버린다면 사이클이 아니게 되고, p_i-1을 두 번 통과하게 되니까요. 즉 p_i는 p_1, p_2, .. p_i-2 중 하나의 점과 연결되어 있습니다. 즉, b_i-1,i는 이 모든 경우 중 거리의 합이 가장 작을 경우를 의미합니다.
이 경우들에서 p_i와 연결된 점을 p_j라고 하면, 여기에서 b_i-1,i 를 구하기 위한 식은 min(b_i-1,j+min(j,i)) (1<=j<j-1)라고 할 수 있습니다. 그런데 우리는 정의에서 i<=j 일 경우만 보겠다고 정의하지 않았나요? 그런데 이 식에서는 반대로 i>j가 되어버리는군요. 그러나 조금만 생각해보면 만약 우리가 바이토닉 투어의 최적값을 구하고 있다면 b_i,j = b_j,i 가 됨을 알 수 있습니다. 거쳐가는 경로는 같고, 가는 방향만 다른데 바이토닉 투어의 거리의 합이 달라지겠어요? 따라서 우리는 b_i-1,i 를 다음과 같은 방법으로 구할 수 있습니다.
이제 두 점이 인접해있지 않을 경우의 b_j,i(j<i-1일 경우) 를 구할 것인데, 조금만 생각해보면 이 값을 구하는 것은 어렵지 않다는 것을 알 수 있습니다. p_i가 p_i-1이 아닌 어떠한 점 p_k와 연결되어 있다고 합시다. 그런데 p_k가 p_j-1보다 왼쪽에 있다면, p_j-1은 누구와 연결되어야 하죠? j의 범위에 의해 p_j가 p_i보다 왼쪽에 있기 때문에 p_i-1을 왼쪽으로 가면서 지나가는 것은 불가능하기 때문에 p_i-1은 무조건 오른쪽으로 진행하면서 지나가야 하는데, p_i가 p_i-1이 아닌 점과 연결되어 있다면 p_i-1는 이 사이클에서 연결될 방법이 없습니다. 즉, P_j,i 는 무조건 P_j,i-1에서 p_i-1과 p_i를 연결한 모습을 띄게 됩니다. 이를 통해 b_j,i 의 값을 구할 수 있습니다.
마찬가지로 b_i,i 도 비슷한 방법을 통해 구해낼 수 있습니다. b_j,i 를 유도할 때와 비슷한 아이디어로 접근하면, p_i-1은 왼쪽으로 가면서 통과하던, 오른쪽으로 가면서 통과하던 간에 p_i와 무조건 연결되어있어야 하므로 P_i-1,i 나 P_i,i-1 에 p_i-1과 p_i를 이은 형태가 될 것이며, b_i-1,i = b_i,i-1 이기 때문에 우리는 다음과 같은 식을 도출해낼 수 있습니다.
지금까지 도출해낸 점화식들을 이용하면 b_1,i 부터 b_i,i 까지의 값을 구해낼 수 있으며, i의 값을 순차적으로 늘려가면서 상향식으로 DP 배열을 채워나간다면 최종적으로 우리가 구하고자 하는 바이토닉 투어 사이클의 최소 길이인 b_n,n 을 쉽게 구해낼 수 있겠지요?
또한 이 알고리즘의 시간복잡도는 O(n^2) 로서, i를 증가시키는 부분이 n, b_i-1,i 를 구하는 부분이 n으로 합하면 O(n^2)의 연산을 하게 됩니다.
실제로 이 문제를 코딩하면서 이해하시기 위한 분은 http://211.228.163.31/pool/bitonic/bitonic.php?pname=bitonic (더블릿) 을 참조하세요. 이 게시물에서 다룬 것과 같이 점들의 위치들이 주어졌을 때 바이토닉 투어의 최소 길이를 구하는 문제입니다. 다만 주의할 점은 문제에서 n이 30 이하, 좌표의 절대값이 100 이하라고 명시되어 있는데, 실제 테스트 케이스에서는 n이 300 정도는 되는 것 같고, 좌표의 절대값도 100은 훨씬 넘어가서 한 10만 정도까지는 오르는 것 같습니다. 이 부분은 적당히 높은 수를 잡아서 해결해주시길 바랍니다.
이 문제에 대한 저의 코드는 아래 요약글에 적어 놓을 테니 혹시 참고하실 분이 있다면 참조해 주시길 바랍니다. 거의 위의 점화식을 그대로 코드로 옮겨놓은 수준이라 참고할 부분이 있을런지는 모르겠습니다만..
#include<stdio.h>
#include<math.h>
#include<algorithm>
double b[305][305];
struct point {
int x,y;
}a[305];
bool comp (point a, point b) { return a.x<b.x;}
double dist (point a, point b) { return sqrt((double)((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y))); }
int main () {
int n,i,j;
scanf("%d",&n);
for(i=1;i<=n;i++) scanf("%d %d",&a[i].x,&a[i].y);
std::sort(a+1,a+n+1,comp);
for(i=2;i<=n;i++) {
double min=100000000; // 범위 내에서 INF
for(j=1;j<i-1;j++) b[j][i]=b[j][i-1]+dist(a[i],a[i-1]);
for(j=1;j<i-1;j++)
if (b[j][i-1]+dist(a[j],a[i])<min) min=b[j][i-1]+dist(a[j],a[i]);
if(min==100000000) min=dist(a[i],a[i-1]);
b[i-1][i]=min;
b[i][i]=min+dist(a[i],a[i-1]);
}
printf("%.2lf",b[n][n]);
return 0;
}
만약 바이토닉 투어의 길이 뿐만이 아니라 실질적인 그래프의 연결 방법도 알고 싶다면, 다익스트라 알고리즘의 역추적 알고리즘처럼 연결된 노드의 번호를 저장하는 배열을 만들어 DP를 갱신할 때 같이 갱신해주는 방법을 사용하면 될 것입니다. 이 부분에 대한 구체적인 논의나 코딩은 이 게시물에서는 생략하겠습니다. 그렇게 어렵지 않으니 직접 코딩해보세요 :)
바이토닉 투어는 DP를 이용하여 TSP에 제한을 건 사이클을 구하는 알고리즘이었습니다. 중요한 점은 이 알고리즘이 다양한 경시대회 문제에서 응용되어 출제되는 경우가 있다는 점입니다. 실제로 제 5회 IOI 에서는 점들이 주어졌을 때 가장 많은 점을 커버하는 바이토닉 투어를 만드는 문제가 출제되었으며, KOI 등의 경시대회에서도 바이토닉 투어의 개념을 응용한 문제가 전국 본선에 출제된 적이 있습니다. 따라서 정보과학 경시대회를 준비하시는 학생 분들이라면 한번쯤은 이해하고 넘어가야할 알고리즘이 아닌가 싶네요.
바이토닉 투어를 응용한 몇 가지의 문제들을 제시해 놓을테니, 이 문제들을 직접 풀어보면서 바이토닉 투어를 응용하는 방법을 익혀보시기 바랍니다.
경찰차 : http://koistudy.net/?mid=prob_page&NO=340 (KOI 03' 중등부 기출)
Comeback vault 101 (from Fallout3) : http://koistudy.net/?mid=prob_page&NO=505 (Iamcoder #2)
다음 포스팅은 언제가 될지 기약할 수는 없지만.. 아마 Dynamical Backtracking에 대한 포스팅이 되지 않을까 싶습니다. 일단 먼저 제가 이 알고리즘에 대해서 완벽히 이해해야겠지만요..
[출처] 바이토닉 투어 (Bitonic Tour)|작성자 유키사
'Algorithm' 카테고리의 다른 글
| 디자인패턴 observer (0) | 2014.10.17 |
|---|---|
| quick sort (0) | 2014.10.17 |
| topological sort (0) | 2014.10.17 |
| 다익스트라 벨만포드 알고리즘 (0) | 2014.10.17 |
| heapsort, insertionsort, quicksort, mergesort (0) | 2014.04.28 |