변수의 기능에 따른 분류
- 독립변수 : 실험에서는 연구자에 의해서 조작되는 변수
- 종속변수 : 영향을 받는 변수, 실험에서는 독립변수의 변화에 따라 나타나는 결과의 예측변수라고도 함
- 통제변수 : 독립변수와 종속변수 간에 영향을 미칠 수 있는 제3의 변수. 실험 과정에서 독립변수와 종속변수의 영향 파악을 위해서 통제해야 하는 변수
- 매개변수 : 독립변수와 종속변수 간에 직접적인 관련은 없으나 중간에서 매개자 역할을 하여 두 변수 간에 간접적인 영향을 맺도록 하는 변수
- 외생변수 : 독립변수와 종속변수 간에 상관관계가 있는 것처럼 보이지만 실제적으로는 관계가 없는데 단지 제3의 변수에 의해서 가상적 관계가 성립되어 있는 것처럼 보이는 변수. 외생변수의 통제를 통해 가식적 관계를 제거해야 함.
- 억압변수 : 독립변수와 종속변수 간에 상관관계가 있는데 없는 것처럼 보이도록 만드는 변수. 가식적 영관계라고 함.
변수의 속성에 따른 분류
- 이산변수 : 하나하나 셀 수 있는 변수
- 연속변수 : 등간 척도나 비율 척도 자료에 해당함
- 더미변수 : 주로 회귀분석을 할 때, 명목형 변수를 독립변수로 사용하고자 할 때 더미 변수화해서 사용함.
대푯값
- 산술평균
- 기하평균 : 변화율 등을 구할 때 사용되는 대표값
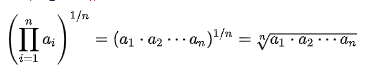
- 조화평균 : 시간적으로 계속되는 형태의 속도 등을 계산할 때 사용
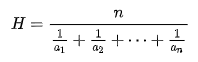
- 중위수 : 자료를 크기 순으로 나열했을 때 중간에 오는 값
- 최빈수 : 빈도가 가장 많은 값. 없을수도 있고 여러개 있을 수도 있음.
- 사분위수 : 자료를 크기 순으로 나열했을 때 4등분한 위치의 값. 1사분위수 : 25% 위치 값, 2사분위수 : 50% 위치 값
- 범위 : 최대값 - 최소값
- 분산 : 평균으로부터 흩어진 정도. 모분산(Var = σ^2), 표본분산(S^2)

- 표준편차 : 분산의 제곱근 값
- 사분위범위 : 제3사분위수 - 제1사분위수
- 변동계수(CV : Coefficient of Variance) : 단위가 다른 변수에 대해서 산포를 비교하고자할 때 사용= (표준편차/표본평균) * 100
대푯값 검정, 평균차이 검정, 쌍체비교
- 깔끔하게 pass
카이제곱

확률표본 추출방법
- 단순 무작위 표본 추출 : 난수표나 컴퓨터를 이용한 난수의 추출방법을 이용하여 표본 추출
- 층화표본 추출 : 모집단을 집단 내 동질적인 몇개의 집단으로 나누고 각 층별로 단순무작위 추출 적용
- 계통표본 추출 : 일정한 순서에 따라 표본 추출(= 체계적 표본 추출)
- 집략표본 추출 : 개별적 표본이 아닌 집략을 먼저 추출한 후 개별적 표본을 추출
비확률표본 추출 방법
- 할당표본 추출 : 연구자의 사전지식을 기초로 하여 모집단의 특성을 나타내는 하위 집단을 기준으로 표본수를 할당하고 추출
- 유의표본 추출 : 모집단에 대한 사전지식을 전제로 연구자 판단에 의해 추출
- 임의표본 추출 : 연구자가 표본 선정에 편리성을 두고 표본을 선정
- 누적표본 추출 : 응답자의 사생활이 보호되는 상태에서 조사가 이뤄져야 한다는 것이 누적표본 추출
상관계수
- r이 0보다 큰 경우 양의 상관관계, 0보다 작은 경우 음의 상관관계

왜도값(=비대칭도)
- 자료의 형태가 어느 쪽으로 기울어져 있는가를 나타내는 통계량
- 왜도값 = (평균-최빈수) / 표준편차 = 3*(평균-중위수) / 표준편차
- 왜도값이 0인 경우 : 평균 = 중위수 = 최빈값
- 왜도값이 +인 경우 : 분포의 모양이 왼쪽으로 기울어진 경우, 최빈값 <= 중위수 <= 평균
- 왜도값이 -인 경우 : 분포의 모양이 오른쪽으로 기울어진 경우, 평균 <= 중위수 <= 최빈값
다중공선성
- 다중회귀분석의 경우 독립변수들 간의 상관관계가 없다는 가정이 필요한데, 이 때 독립변수 간에 상관관계가 존재한다면 다중공선성이 존재한다는 의미이다.
다중공선성 문제 해결 절차
- 회귀분석에서 독립변수들 간의 상관관계를 구하여 의심
- 분산팽창지수를 계산
- 분산팽창지수(VIF)가 10 이상이면 독립변수들 간에 상관관계가 있다고 판정.
(281p - 289p 문제 풀이 필요)
데이터 전처리
- 데이터 필터링 : 분석목적에 맞는 데이터만 추출, 오류나 중복 제거, 저품질 개선
- 데이터 유형변환 : 분석목적에 맞게 데이터 형태를 변환
- 데이터 정제 : 결측치를 처리하거나 불일치 교정, 노이즈 데이터 처리
데이터 후처리
- 데이터 변환 : 수집된 데이터를 일관성 있는 형식으로 변환하는 것
- 데이터 통합 : 연관성 있는 데이터를 결집, 연관관계분석 등을 통해 중복데이터를 검출하고 데이터 단위를 일치시키는 것
- 데이터 축소 : 분석에 불필요한 데이터를 축소하여 분석의 효율성 높이는 과정
베르누이 시행
- P(S) = p, P(F) = 1-p, 여기에서 S는 성공, F는 실패
- E(X) = p, V(X) = pq
이항분포
- 베르누이 시행을 n번 독립적으로 반복할 때의 확률변수 X는 모수 (N, P)인 이항분포를 따름
- E(X) = np, V(X) = npq
포아송 분포
- 단위시간 당 또는 단위면적 당 사건의 평균 횟수가 몇번인지를 확률변수 X로 정의
- E(X) = λ, V(X) = λ

초기하분포
- 유한모집단에서 비복원 추출의 경우 성공의 수를 확률변수 X로 정의한다면 확률변수 X의 분포가 초기하분포가 됨.
기하분포
- 첫번째 성공이 일어날 때까지 시행 횟수를 가지고 확률분포를 설명할 경우 기하분포라고 한다.
- E(X) = 1/p. V(X) = q/p^2
t분포
- 표본 크기가 작을 때, 즉 n<30인 경우 평균차이를 비교하기 위해 주로 이용
카이제곱분포
- 범주형 변수에 대해서 두 변수 간 연관성 검증을 위해서 사용되는 분석기법(x^2)
F분포
- 세 집단 이상의 평균차이 검정에 주로 사용되어지는 통계량
중심극한정리
- 모집단의 분포가 정규분포가 아닌 경우는 X의 분포는 모집단의 분포에 따라 다르게 나타나는데 표본 크기 n이 큰 경우는 표본평균 X의 분포는 모집단의 분포와 상관없이 정규분포로 근사하게 되는 성질
모평균에 대한 점추정
- 추정량 = 표본집단에서의 표본평균 x
- 표준오차 = S.E(X) = σ/n^1/2
편의
- 표본 추출에서 추정되는 모수와 추정량의 기댓값과의 차이
시계열 자료에 대한 잔차 진단 방법
- 잔차 : 예측값과 실제값 사이의 차이를 의미
- 자기상관 : 잔차에 자기상관이 없어야 좋은 모델. 잔차에 대한 조건은 평균이 0이어야 함. 아닌 경우 예측값이 편이가 생길 수 있으며 잔차의 분산은 상수가 되도록 잔차의 분포는 정규분포를 따르도록 한다.
시계열 모형
- 자기회귀모형(AR모형) : 현 시점의 자료를 p 시점 전의 과거 자료로 설명이 가능
- 이동평균모형(MA모형) : 현 시즘의 자료를 유한개의 백색잡음의 선형 결합으로 표현하고 항상 정상성을 만족하므로 정상성의 가정이 따로 필요 없는 모델
- 자기회귀 누적이동평균모형(ARIMA모형) : 비정상 시계열 모형이기 때문에 차분이나 변환을 통해 AR 모형이나 MA모형으로 정상화함.
비모수 검정
- 부호검정, 윌콕슨 순위합 검정, 크루스칼-왈리스 순위검정, 런검정,
상관분석
- 상관계수를 제곱하면 결정계수이다. 결정계수가 크다는 것은 회귀식의 설명력이 높다.
- 상관계수의 부호는 공분산의 부호와 같다. 상관계수의 부호와 회귀식 부호는 같다.
- 두 확률변수가 독립이면 상관계수는 0이다. 상관관계가 0이면 두 확률변수가 독립이라는 역은 성립하지 않음.
- 변수들 간의 유사성을 알아보기 위해 상관관계 행렬을 사용
요인분석
- 많은 변수의 수를 줄여서 요인으로 차원을 축소하는 통계분석기법
- 변수가 정규분포를 따라야 하며, 표본의 수는 변수의 4~5배 정도가 되어야 함
- 변수의 차원을 줄이는 방법으로 다변량회귀분석, 다변량분산분석, 주성분분석, 요인분석, 정준상관분석이 있음
- 케이스의 차원을 줄이는 방법으로 군집분석, 판별분석, 다차원척도법이 있음
'Programmer's' 카테고리의 다른 글
| 빅데이터 분석기사 요약 - 4과목. 빅데이터 결과 해석 (0) | 2021.04.16 |
|---|---|
| 빅데이터 분석기사 요약 - 3과목. 빅데이터 모델링 (0) | 2021.04.16 |
| 빅데이터 분석기사 요약 - 1과목. 빅데이터 분석 기획 (0) | 2021.04.15 |
| tnas os에서 python3 (0) | 2021.01.27 |
| tnas(f2-210) os에서 pip 사용하기 (0) | 2021.01.27 |